Research
Research interests:
- Discretisation of integrable systems
- Integrability of birational discrete dynamical systems
- Semitoric integrable systems and their classification
- Symplectic invariants of singular Lagrangian fibrations
- Geometric aspects of dynamical systems
- Bifurcation of ordinary differential equations
Other topics I am interested in and would like to learn more about are: data-driven modelling, time-series analysis, machine learning, complex systems and models with differential equations in physics and finance.
Research summary:
Dynamical systems
Dynamical systems are mathematical models that describe the evolution of systems with time, such as the motion of a pendulum, the changes in fish populations, the concentration of a certain chemical in a solution or the electric field variations inside a neuron. At any given moment, the state of a dynamical system is identified with a point in a state space, the so-called phase space. By studying the geometry of this space, we can determine qualitative aspects of the evolution of the system. Some typical questions that we try to answer are:
- Are there any stationary states, such as equilibrium points?
- Can we find some periodic behaviour or the system keeps changing indefinitely?
- What does the system look like after a great amount of time has passed?
Completely integrable systems
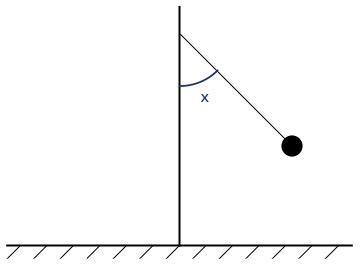
There are two main types of dynamical systems: continuous and discrete. Continuous dynamical systems are models that consider time as a continuous variable and are often defined by differential equations. Discrete dynamical systems, on the contrary, regard time as a discrete variable, so evolution happens in “steps”, represented by repeated applications of a given map.
In certain occasions, some physical quantities of a dynamical system, such as the energy and angular momentum are preserved. This simplifies the study of these systems, either continuous or discrete, since we know that solutions must stay within the same energy level. So we can use methods from symplectic and algebraic geometry to study these level sets. This idea can be generalised to systems with 2n-dimensional state spaces and n conserved quantities, known as completely integrable systems. Harmonic oscillators, the spherical pendulum or the Euler top are all examples of this type.
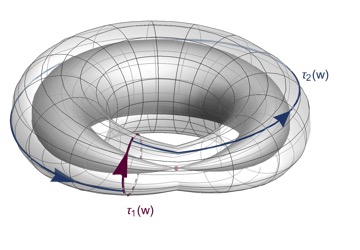
Discretisation of integrable systems
Discretisations are techniques for obtaining a discrete dynamical system out of a continuous one. There exist several types of discretisations, depending on what characteristics we want the resulting system to have. In particular, one can ask whether a given discretisation method preserves integrability, that is, whether given an integrable continuous dynamical system, it returns an integrable discrete dynamical system. One method that seems rather good at this task is the so-called Kahan discretisation for quadratic vector fields, introduced by W. Kahan. The systems obtained with this method are often integrable, though not always. Part of my research focuses on finding how we can improve this method to ensure that the resulting system always preserves integrability.
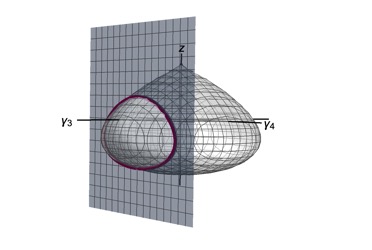
Semitoric systems
Another question related to integrability is the following. In line with M. Kac’s famous paper entitled “Can we hear the shape of a drum?”, one can ask how much of the properties of an integrable system are retained in its energy values. A good example is that of so-called toric systems, for which the conserved quantities define an effective n-dimensional torus action. T. Delzant showed that these systems can be completely classified in terms of certain polytopes, which correspond to the set of possible energy values.
Inspired by this situation, Á. Pelayo and S. Vũ Ngọc found in the recent years a global classification for a certain class of integrable systems with a 4-dimensional state space, called semitoric systems. These systems have two compatible conserved quantities, but only one of them comes from a rotation symmetry. The classification is based on five invariants and it is relevant because such systems appear often in physics, among others as classical counterparts of quantum systems.
Part of my research focuses on the computation of these invariants for some families of systems that depend on several parameters with the help of powerful mathematical software such as Mathematica. We have shown how the invariants convey this dependence on the parameters and also how they display the symmetries of the systems. This is crucial in order to understand the meaning and the properties of these invariants. Together with my collaborators in Australia, Belgium and the US, we aim at a better understanding of semitoric systems in general and the nature of their symplectic invariants.